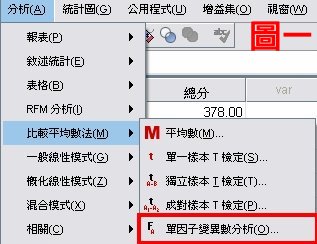
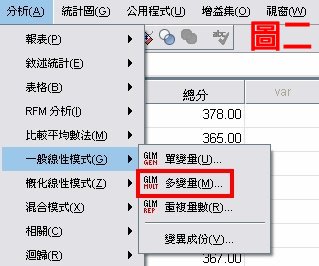
這篇是統計方法選錯了嗎？ANOVA與MANOVA!的驗證版，實際使用統計結果來比較ANOVA與MANOVA的不同，圖一顯示單因子變異數分析位於SPSS分析>比較平均數法裡面；而圖二顯示多變量變異數分析位於SPSS分析>一般線性模式裡面。
以下看到的範例的研究問題如下：
研究目的：國小六年級學生的學業成績，是否會因為性別而有差異？
1.國小六年級學生的國語成績，是否會因為性別而有差異？
2.國小六年級學生的數學成績，是否會因為性別而有差異？
3.國小六年級學生的自然成績，是否會因為性別而有差異？
4.國小六年級學生的社會成績，是否會因為性別而有差異？
5.國小六年級學生的整體學業成績，是否會因為性別而有差異？
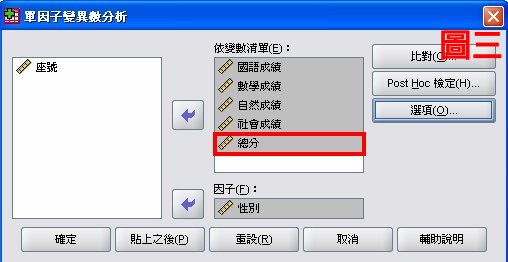
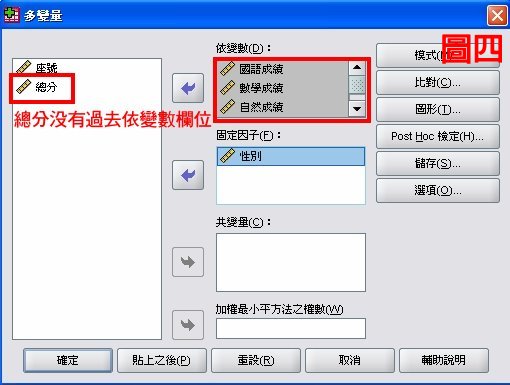
圖三為單因子變異數分析的功能視窗，很多研究生會把四科成績加總成總分，所以在依變數欄位裡面的五個依變數就分別用來解釋上述的五個待答問題；但是從圖四多變量變異數分析的功能視窗來看，總分這個變數不需要被選入依變數的視窗，因為多變量變異數分析會根據四科成績，先出現整體學業成績是否有差異，再出現各科的F值。這裡出現一個大家要思考的問題，用ANOVA來分析總分能夠得出真正的結果嗎？總分真的就是整體學業成績的意思嗎？大部分的研究生都是這樣的作法喔！
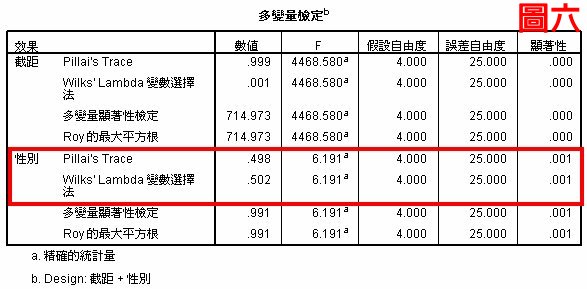
圖五顯示ANOVA的分析結果，男女在國語與數學有顯著差異的存在，而總分並沒有顯著差異（p=.960>.05）；而圖六與圖七為多變量變異數分析的統計結果，圖六紅色框起來的結果就是第五個待答問題的答案，當變異數不同質時，我們看Pillai’s Trace值，當變異數同質時，我們看Wilks’ Lambda值，無論是哪個數值（p=.001<.01）都顯示性別在整體學業成績是有顯著差異的，這個結果與ANOVA在總分的分析結果是不一樣的，總分真的能夠代表整體嗎？總分為什麼成為第五個依變數呢？我想應該不行，這個結果是不是代表有很多研究生跑錯統計方法了！
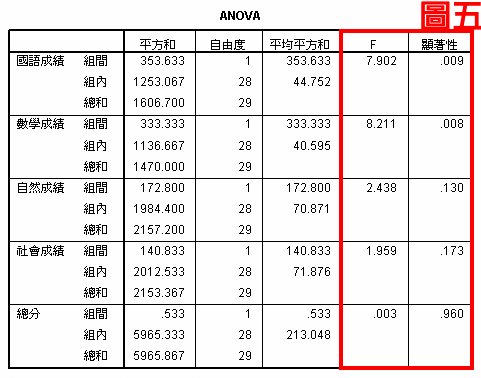
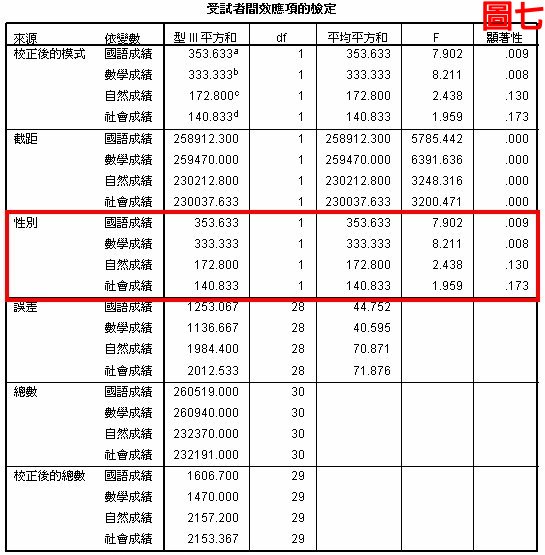
圖七是多變量變異數分析的各科F值，大家有沒有發現F值與圖五ANOVA的F值都一樣，其實MANOVA把ANOVA包含在裡面了，所以以後遇到類似的問題，聰明如您，會選擇ANOVA還是MANOVA呢？
