統計方法選錯了嗎?ANOVA與MANOVA!
文章目錄

壹、前言
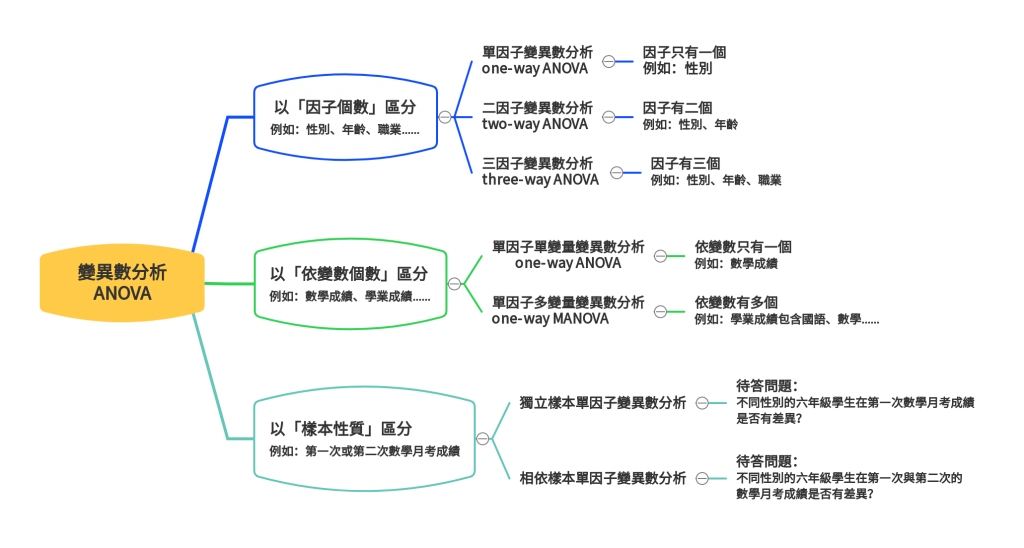
十年前在研究所讀書的時候,說到量化研究…大家最朗朗上口的統計方法就是ANOVA,似乎在論文裡面沒有ANOVA,論文就寫不下去了,ANOVA俗稱為單因子變異數分析,而單因子變異數分析可因為 「因子個數」的不同,而分為「單因子變異數分析」、「二因子變異數分析」,甚至是「 三因子變異數分析 」;也可以因為「依變數數量」的不同,而分為「單因子單變量變異數分析」與「單因子多變量變異數分析」;也可以因為「樣本性質」的不同,又分為「獨立樣本單因子變異數分析」與「相依樣本單因子變異數分析」,變異數分析家族如下圖1所示。以下針對「單因子單變量變異數分析」與「單因子多變量變異數分析」的採用時機進行討論說明如下。
貳、單因子單變量變異數分析(one-way ANOVA)
以下範例以「數學成績」為依變數,數學成績是單科成績,所以是單變量變異數分析。
獨立樣本範例:
當我們想要瞭解國小六年級學生的數學月考成績,是否會因為學校規模(大、中、小)而有差異?
此時「學校規模」為因子,「數學成績」為依變數,而六年級學生的數學成績為各自獨立的樣本,所以要比較六年級學生的數學成績是否因為「學校規模」而有高低差異,我們就要進行「獨立樣本單因子單變量變異數分析」。
相依樣本 範例:
當我們想要瞭解國小六年級學生的數學月考成績,在期初、期中與期末是否有差異情形?
此時不同時間進行的月考就是因子,但這三次的數學月考成績都是同一組人,所以樣本並不是互相獨立,而是相依樣本,所以要比較高低差異,我們就要進行「相依樣本單因子單變量變異數分析」。
參、單因子多變量變異數分析(one-way MANOVA)
除了ANOVA,其實還有另外一種變異數分析-「多變量變異數分析」,ANOVA考驗的是單一依變數在各組平均數的差異,而多變量變異數分析卻可以同時考驗多個依變數各組平均數的差異,且單因子多變量變異數分析亦可分為「獨立樣本單因子多變量變異數分析」與「相依樣本單因子多變量變異數分析」,舉例說明如下:
以下範例以「學業成績」為依變數,學業成績為包含國語、數學、自然與社會四科的總成績,此時的依變數變成四個,不像上面的數學成績是單科成績,所以變成多變量變異數分析,以下舉例說明:
獨立樣本範例:
當我們想要瞭解國小六年級學生的學業成績,是否會因為學校規模(大、中、小)而有差異?
此時學校規模就是因子,不同學校規模六年級學生的學業成績為各自獨立的樣本,但是學業成績包含國語、數學、自然與社會四科的成績,所以要比較學業成績的高低差異,比較完整的作法是將四科做為四個依變數,同時一起進入變異數分析,此時的分析方法就是「獨立樣本單因子多變量變異數分析」。
相依樣本範例:
當我們想要瞭解國小六年級學生的學業成績,在期初、期中與期末是否有差異情形?
此時不同時間進行的月考就是因子,但這三次的月考成績都是同一組人,所以樣本並不是互相獨立而是相依樣本,而且學業成績同時包涵國語、數學、自然與社會四科的成績,所以要比較學業成績的高低差異,就要進行「相依樣本單因子多變量變異數分析」。
肆、針對待答問題,正確選用單變量或多變量
最後,擺脫上述範例,我採用某論文的一個研究問題與五個待答問題,分別進行比較並說明其適合採用的變異數分析方法,研究問題如下:
不同學校規模的國民小學教師,其知覺之組織變革是否具有顯著差異?
(組織變革分為行政、教學、制度與文化四個層面)
待答問題衍生如下:
1.不同學校規模的國民小學教師,其知覺之行政變革是否具有顯著差異?
2.不同學校規模的國民小學教師,其知覺之教學變革是否具有顯著差異?
3.不同學校規模的國民小學教師,其知覺之制度變革是否具有顯著差異?
4.不同學校規模的國民小學教師,其知覺之文化變革是否具有顯著差異?
5.不同學校規模的國民小學教師,其知覺之整體組織變革是否具有顯著差異?
上述五個待答問題是從一個研究問題分出來的,其中1-4題跑ANOVA(單因子單變量變異數分析)是沒問題的,問題點出在第5個待答問題,大部分的碩士論文將填答者在四個層面的得分進行加總,利用總分來跑ANOVA,然後利用結果來回答整體組織變革在不同學校規模教師是否具有顯著差異,如果總分沒有顯著差異,那麼研究者可能就會做出不同學校規模的國小教師,其知覺之整體組織變革沒有顯著差異,可是大家有沒有想過,有沒有可能其中的行政變革與教學變革有顯著差異,但是因為總分加起來差不多,所有整體組織變革沒有顯著差異!
舉例來說:
如果大校的教師在「行政變革」層面的平均分數為3.2(五點量表計分),而小校的教師在行政變革為4.1分;而大校的教師在「教學變革」層面的平均分數為4.2分,小校的教師在「教學變革」的平均分數為3.3分。(故意假設大校與小校在這兩個層面的得分高低剛好相反)
平均數差0.5就差很多了,所以大校與小校教師這兩個層面的單因子單變量變異數分析(ANOVA)一定會有顯著差異存在,結果應是小校教師在「行政變革」顯著高於小校教師,而大校教師在「教學變革」顯著高於小校教師,但是這時候如果其他兩個層面沒有太大差異的話,那將四個層面加總作為總分進行單因子單變量變異數分析,上述第5個待答問題「不同學校規模的國民小學教師,其知覺之整體組織變革是否具有顯著差異? 」的分析結果,會因為行政變革與教學變革得分的差異互相抵銷了,所以會得到「不同學校規模之國小教師在整體組織變革沒有顯著差異存在」的結論。
但這樣的結論是對的嗎?如果不將四個層面進行加總,而是將四個層面作為四個依變數進行單因子多變量變異數分析,其實會得到 「不同學校規模之國小教師在整體組織變革有顯著差異存在」的相反結論 ,試想如果利用總分跑單因子單變量分析,結論是整體沒差異,但是其中兩個層面有差異,這樣子的結論是不是怪怪的。
相對的,如果整體的差異分析利用單因子多變量變異數分析,那麼結論就會變成整體有差異,而且這個差異來自於行政變革與教學變革,而且小校教師在「行政變革」顯著高於小校教師,而大校教師在「教學變革」顯著高於小校教師,這樣的結論是否更好呢?
伍、單變量還是多變量,選對了嗎?
單變量還是多變量,有關於整體或總分的觀念極待釐清,總分能夠代表整體嗎?舉例來說:某兩群學生其學業成績總分相差不多,以ANOVA進行變異數分析,所以沒有顯著差異,但是有沒有可能某一群學生的數學成績較高,國語成績較低,而另一群學生恰好相反-數學較低、國語較高,所有造成這兩群學生的加起來的總分相差不多,但是說不定他們的國語與數學成績是有顯著差異的,或許我們下另外一個結論會更好:這兩群學生的學業成績有顯著差異,且這差異來自於國語與數學,惟總分並沒有差異存在。
所以,我認為不能用加總的總分來代表整體表現(用在升學成績可以,但論文統計未必),整體表現要從構成變數的層面來討論,例如:我們要探討組織變革,就要從其構成的四個層面一起來做探討,我們要探討學業成績也要從構成學業成績的四個科目來探討。所以,ANOVA只能處理單一依變數的差異比較,但是MANOVA卻能將多個依變數同時處理,得出其整體差異情形,再依次探討個別依變數是否有差異,也就是ANOVA其實就包含在MANOVA裡面了,ANOVA只能將層面一一分開討論,好像他們彼此不相關似的,而MANOVA卻是從整體先看,再個別一一來看;講到這裡,感覺有許多碩士論文似乎選錯變異數分析的統計方法了!
本文2022/06/22 第一次更新
想看更多的統計文獻嗎?請到本站常見統計分析相關文獻引用大全(陸續增加中……)




1 comment